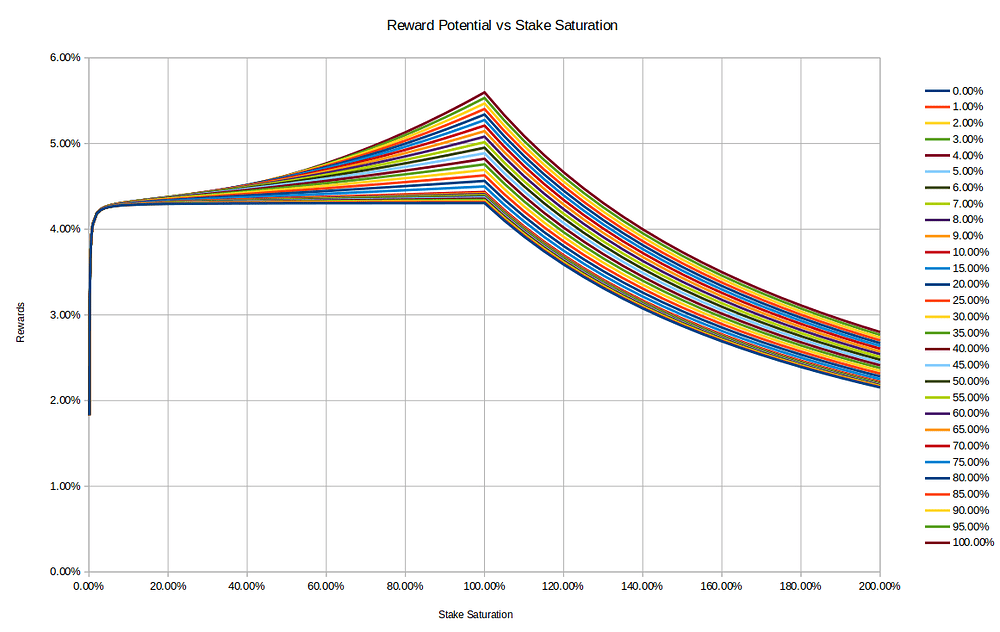
Team,
As promised here are charts. This is the current reward level as a function of pool saturation at various pledge fractions from 0% to 100%. a0=0.3 and minFee=340.
Clearly being a whale and pledging to a private pool is what the reward formula was designed to favor.
Most operators have far less than 20% pledge so multipools have become favored for operators.
What happens if we drop minFee to 30?
Whales which pledge into private pools still earn higher rewards.
It is far easier for small pools to provide competitive yields exceeding 4% (on average).
What happens if we keep minFee=30 and increase a0 to 0.5?
Yields would drop for most people and only a couple dozen ultra-whales would retain yield.
Increasing a0 clearly only benefits ultra-whales pledging to private pools.
What happens if we keep minFee=30 and drop a0 to 0.1?
Yields increase (4.2% to 5.1% for most people) and the ultra-whale advantage decreases to a half percent.
Decreasing a0 to 0.0 removes the ultra-whale advantage entirely and most of the reward equation.
For now, let’s discuss and debate the principles of the Cardano reward equation.
- Do we want ultra-whale pledge to have a yield advantage? 0.0% 0.5% 1.0%?
- How harsh of an on-ramp do we want?
- What should diminishing rewards based on stake look like? (currently based on k)
- What should diminishing rewards based on pledge look like? (Nothing yet)
- Should a0 be transformed from the ultra-whale boost parameter to a complement of k but for pledge? (would require a new equation and hard-fork, however no new parameters)
Other Open Items:
- Rename k-effective for @Colin_Edwards ?
- I will be happy to lead creating an equation and CIP based on our principles with diminishing rewards for stake (based on k) and diminishing rewards for inadequate pledge (a refactored a0).